Revista Saberes
Preocupadas por la dificultad que manifestaban los estudiantes a la hora de dividir, ya sea como ejercicio o en el contexto de una situación problemática, cuatro profesoras de ISFD realizaron una investigación diagnóstica sobre las diversas técnicas de resolución de esa operación matemática, en el primer año de la escuela secundaria. Las diferentes metodologías y la falta de articulación con la enseñanza primaria, temas de indagación.
“La idea surge a partir de una inquietud común ya que algunas de nosotras trabajábamos en primer año del secundario y cuando abordábamos la división podíamos visualizar diversas técnicas de resolución, algunas de las cuales no eran conocidas por otras docentes”, señala Mariel Mondino, autora junto a Silvana Rainero, Pamela Demaria y María Laura Magliano, de la investigación realizada en el marco de un proyecto de articulación entre la Dirección General de Educación Superior de la cartera educativa provincial y la Universidad Nacional de Córdoba. “Las cuatro integrantes del equipo somos profesoras de Matemática y nos interesaba comprender el trabajo que se hace, en la construcción del cálculo de la división, en primaria y qué sucede con ello en la secundaria”, señala Mondino, acerca de la indagación realizada en el marco de la línea “Entramando la matemática y las prácticas educativas para el fortalecimiento de la enseñanza e investigación en Matemática y Educación Matemática”.

Para el estudio Las técnicas de cálculo de la división de números naturales en la transición entre la escuela primaria y secundaria, se seleccionaron tres cursos de primer año de dos instituciones educativas de la ciudad de San Francisco, como muestra. Lo interesante de esta elección radica en que ninguno de los dos establecimientos educativos cuenta con nivel primario. De allí que la población estudiantil que albergan proviene de diferentes barrios de la ciudad y de distintas localidades de Córdoba y Santa Fe. Las variadas trayectorias escolares de los alumnos permitirían anticipar posibles diferencias didácticas y pedagógicas, a la hora de resolver esta operación matemática, que es una de las más complejas de enseñar y que requiere ser abordada a lo largo de toda la primaria.

Algoritmo convencional.
En relación con la metodología, el primer paso consistió en diseñar un instrumento de evaluación diagnóstica, para acceder a las distintas técnicas empleadas por los estudiantes. Luego se realizaron entrevistas semiestructuradas a los docentes de cada uno de los cursos participantes, donde se incluyó una evaluación que permitiera documentar, según sus experiencias, qué técnicas de cálculo esperaban encontrar en los chicos, cuáles eran las decisiones pedagógicas que habitualmente tomaban a partir de ello y qué cambios realizarían en las consignas, tras el diagnóstico inicial presentado.

Variación del algoritmo convencional por explicitación de la resta y cálculos auxiliares (4 x 2 y 4 x 3).
Con posterioridad, las investigadoras llevaron a cabo dos talleres con los profesores en los que se analizaron algunos aspectos del trabajo realizado: distintas resoluciones de los alumnos y la relación del docente con la enseñanza de la división. A partir de la lectura de material bibliográfico y la sistematización de los diagnósticos, se elaboró una primera categorización que posibilitó agrupar dichas técnicas.
De todo, como en botica

Técnica por descomposición o cocientes parciales (aquí no se consideran las decenas, centenas, etc., sino que se toma el número como una cantidad global).
Luego de analizar todas las formas de resolución realizadas tanto por los chicos como sus profes, se pudieron reconocer ciertas técnicas de cálculo de la división de números naturales que variaron entre divisiones con el algoritmo convencional (figura 1) y con la explicitación de la resta y cálculos auxiliares (figura 2), la técnica por descomposición o cocientes parciales (figura 3) y otra que combina distintos métodos. “En relación a las resoluciones del problema que presentamos a los chicos, también se observaron técnicas multiplicativas y combinación de técnicas aditivas, sustractivas y multiplicativas (figura 4). Tenemos la idea de profundizar en esto más adelante”, señala Rainero.

Resolución del problema donde combina técnicas aditivas, sustractivas y multiplicativas (se observa: adición, sustracción y producto. Obtiene la respuesta al sumar mentalmente, ya que no está registrado, 10 + 8 = 18 cuotas).
En una primera instancia, los docentes plantearon que, por una cuestión de dominio, el método convencional (el del algoritmo, expresado en la figura 1) les resulta el más fácil y rápido y es hacia donde tratan de “empujar” a sus estudiantes por entender que es el más sencillo. Luego, a través de los talleres, los docentes pudieron observar las diferentes “convenciones” presentes en las distintas técnicas de cálculo (realizadas por ellos, por los estudiantes y a través del tiempo: la división egipcia, el método Gerbert, y por galera). “Esta aproximación histórica les permitió redescubrir sus técnicas personales de resolución y también la de los alumnos”, señaló Rainero. “Más allá de cada método, lo más significativo, −explica Magliano− es que los profesores pudieron advertir el carácter relativo y variable de las técnicas de cálculo a lo largo del tiempo y reconocer así que son convenciones sociales y no tan diferentes unas de otras: las históricas de las nuestras, de las de los chicos y que detrás de cada una de ellas existe matemática puesta en juego”. “Su carácter convencional es una valoración vinculada al modo en que aprendimos a resolver la división en la escuela, a lo que nos resulta familiar porque así nos los enseñaron o porque lo usamos habitualmente”, afirma Magliano, lo que implica que esas maneras no son ni absolutas ni para todos iguales, porque dependen de nuestras trayectorias.
En el aula
Cuando los chicos ingresan a primer año se espera que resuelvan correctamente las divisiones, tengan control en los pasos que realizan y que progresivamente puedan realizar estas operaciones del modo más económico. No obstante, “en las prácticas áulicas observamos frecuentemente las dificultades que manifiestan los estudiantes cuando se enfrentan a la resolución de la división como ejercicio o en el contexto de un problema”, señala Silvana Rainero.
“Ante el panorama de diversidad de técnicas encontradas, la investigación nos permitió ver que el docente de primer año toma decisiones que influyen directamente en la gestión de sus clases, que van desde aceptar todo tipo de técnicas para la resolución de la división hasta imponer la unificación en el método o algoritmo convencional que asegure una base de cálculo eficaz en contenidos de mayor complejidad”, explica Mondino. “Pero la dificultad no radica en la diversidad de técnicas de cálculo de la división, sino en el nivel de dominio de cualquiera de ellas”, indica Pamela Demaria al tiempo que Magliano amplía: “Algunos estudiantes no lo tienen y cuentan con escasos recursos de control y análisis de los procedimientos”. En este sentido, la variedad no debería ser un inconveniente sino una oportunidad, en la medida que muestra diferentes caminos que cargan de sentido al cálculo para que este no sea solo una regla a memorizar. De lo que se trata es de implementar estrategias de enseñanza que permitan a los chicos desarrollar las operaciones adecuadas para llegar a un método abreviado, desde distintas vías.
Así, el trabajo de investigación —según señala entre sus conclusiones— permitió, además de descubrir ciertas técnicas de cálculo, “el aporte a la concientización de la matemática que ellas presentan y que muchas veces no son tenidas en cuenta por la naturalización a través de la cual se trabaja dicho contenido en las horas” de clase.
Así, el estudio pretende servir de insumo —tanto a los docentes que enseñan matemática en primaria o en secundaria, como quienes están en los profesorados— para presentar situaciones problemáticas contextualizadas, que tengan en cuenta los conocimientos previos de los chicos y fomenten la socialización de los diversos procedimientos de resolución. Se propone el trabajo con desafíos matemáticos desde primer grado, la presentación de actividades resueltas para que los estudiantes corrijan y así poder analizar las diversidad de técnicas, y finalmente, la realización periódica de reuniones de articulación entre niveles, a fin de acordar los saberes básicos que deben alcanzar los estudiantes, el vocabulario específico a utilizar, criterios de evaluación, además de compartir material de trabajo.
En definitiva, de lo que se trata es de lograr —cuestión que todo docente quiere— que “los alumnos puedan disponer de una técnica eficaz en el cálculo de la división”, tal como resume Demaria.
Fuente:https://revistasaberes.com.ar/2019/10/divide-y-reinaras/
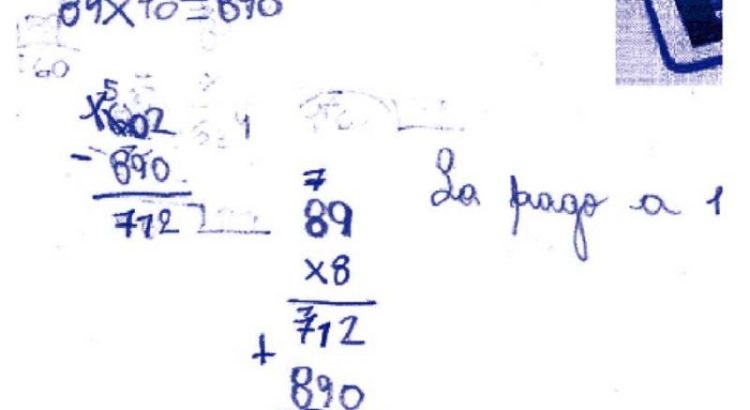





 Users Today : 16
Users Today : 16 Total Users : 35460369
Total Users : 35460369 Views Today : 23
Views Today : 23 Total views : 3419123
Total views : 3419123