Por: Rodolfo Bueno
Una paradoja es una declaración no contradictoria que contradice el sentido común, en ella se unen dos ideas opuestas que contienen una verdad oculta. Las paradojas se dan en cualquier idioma porque todo lenguaje es contradictorio.
Epiménides, filósofo griego del siglo VI antes de Cristo, de quien se dice que durmió durante cincuenta y siete años seguidos, aunque Plutarco sostenga que sólo fueron cincuenta, afirmó que todos los cretenses eran mentirosos, como él mismo, que era cretense, ¿decía o no la verdad? Si lo que dice es cierto no todos los cretenses son mentirosos, porque por lo menos un cretense, él, no miente, o sea que Epiménides miente al decir la verdad; en cambio, si él miente significa que no todos los cretenses mienten, por lo que ha dicho la verdad, o sea que dice la verdad al mentir. Otra versión de esta paradoja, atribuida al filósofo griego Eubulides de Mileto, sostiene: “Si un hombre afirma que está mintiendo. ¿Dice la verdad o miente?” También es contradictoria la afirmación que sostiene, “todo lo que afirmo es mentira”.
Zenón de Elea ideó la paradoja de Aquiles y la tortuga. Aquiles decide competir contra una tortuga. Puesto que él corre rápido le da a la tortuga una ventaja inicial, pues está muy seguro de su fortaleza. Poco después de la partida, Aquiles recorre la distancia que inicialmente lo separaba de la tortuga, pero al llegar a ese lugar descubre que la tortuga ha avanzado un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo adonde estaba la tortuga, ésta ha avanzado un poco más. Por esa causa, Aquiles no ganará la carrera ya que la tortuga estará siempre delante de él.
Se dispara una flecha. Puesto que al mismo tiempo la flecha no puede estar en dos lugares diferentes, la flecha debe hallarse en una determinada posición, por lo que se encuentra en reposo. Por igual razón, durante los siguientes lapsos de tiempo la flecha también estará en reposo; de esta manera, la flecha estará siempre en reposo y su movimiento es imposible. Lo mismo se puede decir de cualquier cuerpo en movimiento, lo que contradice la realidad.
“Vísteme despacio, porque estoy de apuro”, dicen que le dijo Napoleón a Josefina.
“Pienso, luego existo”, escribió Descartes. Luego, si Descartes no piensa, ¿no existe?
“No hay mal que por bien no venga”, es un decir del pueblo.
Hay otras curiosidades matemáticas. En un país habitado por negros y blancos, los primeros sólo dicen la verdad y los segundo siempre mienten. Pasa una canoa y alguien que no distingue el color del canoero le pregunta: “¿Es usted negro o blanco?” La respuesta se la lleva el viento. “¿De qué color dijo que era?”, le pregunta a los dos canoeros que reman detrás. “Dijo que es blanco”, responde el blanco; “dijo que es negro”, responde el negro. ¿De qué color era el canoero? Independientemente del color del canoero, la respuesta es que el canoero era negro.
Una persona es calva si carece de pelos. ¿Qué pasa si tiene sólo un pelo? ¿Si tiene dos?, etc. En general, ¿cuándo un calvo deja de ser calvo?
El director de una cárcel decide liberar a un preso de tres condenados. Coge dos discos azules y tres rojos y sitúa al azar un disco en la espalda de cada preso, de manera que todos ven el color de los demás a excepción del suyo propio. Dejará libre al primero que acierte el color que porta. Pasado cierto tiempo, uno de los presos afirma que el color de su disco es rojo. ¿Cómo lo dedujo, si este preso es ciego?
De antemano se pide disculpas al lector creyente, de cualquier fe que tuviere, porque en este escrito no se intenta jugar con la fe de nadie, muy respetable por cierto, sino que tiene que ver con lo contradictorio que es cualquier idioma. Aclarado este pequeño e importante detalle, se continua con el tema.
Se pregunta: ¿Qué pasa si un objeto superpotente, creado por Dios, capaz de remover todo lo que obstruya su paso, choca contra un objeto inamovible, también creado por Dios? Esto es algo imposible de responder. También es contradictoria la pregunta que durante en el medioevo hacían los herejes a los creyentes: ¿Puede crear Dios una piedra tan pesada que no la pueda levantar? Si no lo puede hacer no es todopoderoso y si la puede crear tampoco lo es. Por esta otra pregunta durante la inquisición fue castigada la persona que la formuló: “¿Tuvo o no tuvo Adán ombligo?” No pudo tenerlo por no ser parido y si no lo tuvo ¿por qué nosotros, que descendemos de él, lo tenemos? También es de por sí contradictoria la idea de que existe un dios omnipotente, amoroso y bueno. Porque si le pidiera algo que sin lugar a duda es bueno y no lo puede hacer, no es omnipotente, si lo puede hacer y no lo quiere hacer, no nos ama ni es amoroso, y si lo quiere hacer y no le da la gana de hacerlo, es caprichoso, se burla de nosotros y no es bueno.
Cada ser humano tiene dos padres, cuatro abuelos, ocho bisabuelos, dieciséis tatarabuelos, etc. Lo que significa que el mundo debió tener mucha más gente antes que ahora, lo que es contradictorio con lo observado y con la idea bíblica de que todos provenimos sólo de Adán y Eva.
El asno de Buridán es el protagonista de un antiguo argumento contra el racionalismo defendido por los partidarios del libre albedrío, que sostenían la posición de que cualquier decisión puede ser tomada de manera racional, y de Juan Buridán, un teólogo escolástico discípulo de Guillermo de Ocán. Para ridiculizar esta opinión, sus críticos imaginaron el absurdo de un asno que no puede elegir entre dos fajos de heno completamente iguales, en consecuencia termina muriendo de inanición. Se trata de que pudiendo comer, no come, porque no sabe, no puede o no quiere elegir qué montón es más conveniente, ya que ambos son exactamente iguales.
Para terminar se hace una pregunta bastante sencilla de responder “¿Qué edad tienen tus hijos?”, pregunta una matemática a una vieja amiga suya. Ésta le responde: “Como recuerdo que eras buena con los números te daré la respuesta a manera de problema. El producto de las edades de mis tres hijos es 36 y la suma es igual al número de ventanas de la casa de enfrente, la blanca”. La matemática, luego de contar las ventanas de la casa de enfrente, afirma: “Me falta un dato”. Ni corta ni perezosa, su amiga se lo da: “El mayor tiene un lunar en la frente”. ¿Qué edad tiene cada muchacho? La pregunta no es tan complicada de responder ahora que se tienen los datos indispensables para despejar todas las incógnitas. Las edades de los niños son 9, 2 y 2 años. Pensemos un poco. Si, por ejemplo, la matemática hubiera contado diez ventanas, habría contestado: “Las edades son 3, 3 y 4 años”, pues 3x3x4=36 y 3+3+4=10, lo mismo en los demás casos. Pero ella ha contado 13 ventanas y en este caso las edades pueden ser 2, 2 y 9, o también, 6, 6 y 1, por lo que dice: “Me falta un dato”, que su amiga le da: “El mayor tiene un lunar en la frente”, o sea, hay hermano mayor, lo que no sucede en 6, 6 y 1, pero sí en 2, 2 y 9. No era tan difícil.
*Fuente: https://rebelion.org/curiosidades-matematicas-2/




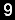
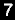
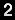
 Users Today : 137
Users Today : 137 Total Users : 35459732
Total Users : 35459732 Views Today : 226
Views Today : 226 Total views : 3418198
Total views : 3418198