Author: Dácil González Martel

¡Disfruta de las matemáticas con cuadernos interactivos!

Dácil González Martel

07 de octubre de 2017 / Fuente: http://blog.tiching.com/

Por: Dácil González Martel

El curso pasado fue el primero en el que empecé a utilizar los cuadernos interactivos en mis clases de matemáticas y la primera conclusión que saqué cuando terminó el curso fue “¿por qué no lo he utilizado antes?”.

Dicho recurso también era nuevo para los alumnos, acostumbrados a utilizar el cuaderno de la asignatura como simple cuaderno de ejercicios donde hacer operaciones y copiar alguna fórmula que otra. Al principio se reían y bromeaban con que parecía más una clase de plástica que de matemáticas, pero poco a poco fueron descubriendo su potencial, poco a poco descubrieron que podían resolver sus propias dudas y las de los compañeros acudiendo al cuaderno de clase, poco a poco dicho recurso tan bueno se convirtió en el mejor compañero de viaje de todos.

Os dejo algunas pautas para empezar a trabajar con los cuadernos interactivos en clase:

  • Empezaremos el cuaderno realizando un índice de contenidos, el cual los alumnos irán rellenando según avance el curso escolar. Dejaremos dos hojas para ello y los alumnos irán escribiendo el nombre del contenido, la página en la que se encuentra y la fecha en la que se dio dicho contenido. De esta forma podrá localizarlo fácilmente en caso de tener que retomarlo más adelante.
  • Dentro de los cuadernos interactivos la página derecha y la izquierda juegan papeles diferentes:
    • La página derecha la utilizaremos para explicar de manera visual, creativa y manipulativa los contenidos a los alumnos. A través de fotocopias, desplegables, dibujos, mapas mentales… El profesor aproximará los contenidos. Al principio siempre es importante poner el título del contenido, la fecha y la página para poder situarlo en el índice de contenidos inicial.
    • La página izquierda será la de trabajo del alumnos, en ella pondrá el mismo título, fecha y página que en la derecha. A continuación se planteará las siguientes preguntas que deberá responder de forma individual:
      • Cuál es la meta de aprendizaje.
      • Qué sé del contenido (se rellena antes de la explicación del profesor).
      • Qué he aprendido (se rellena al finalizar el tema o contenido).
      • Prueba o demostración (inventar un ejemplo práctico del contenido).
      • Reflexión o experimento. Esta es la parte más creativa, en la que el alumno debe poner en práctica lo aprendido extrapolándolo más allá de la asignatura y de manera visual a través de un dibujo, cómic, canción, regla nemotécnica, modelo 3D…
    • Al finalizar la página izquierda (finalizar el tema) pediremos al alumno que en la esquina superior izquierda utilice el semáforo de la comprensión, en el que un punto verde significa que el contenido ha sido fácil y no ha presentado dificultades, un punto amarillo significa que se han presentado algunas dificultades pero finalmente lo ha logrado entender, y un punto rojo significa que aún presenta dificultades para entender el contenido. Esto ayudará al profesor a la hora de la evaluación y el refuerzo de contenidos más complicados.

Los cuadernos interactivos se pueden utilizar en todas las asignaturas, favorecen la autonomía del alumno, su capacidad crítica y le ayuda a construir sus propios conocimientos. Es un recurso en el que las nuevas tecnologías no juegan ningún papel y en el que la parte manipulativa y creativa juega un papel fundamental.

Fuente artículo: http://blog.tiching.com/disfruta-de-las-matematicas-con-cuadernos-interactivos/

cuadernos_interactivos-547×280

Comparte este contenido:
Leer más »

Inteligencias múltiples y matemáticas

Dácil González Martel

27 de septiembre de 2017 / Fuente: http://blog.tiching.com

Por: Dácil González Martel

Teniendo en cuenta la Teoría de las Inteligencias Múltiples de Howard Gardner, en la que manifiesta que la inteligencia es una capacidad, no innata, y que la educación puede desarrollarla y potenciarla, vamos a  hacer una propuesta de cómo podemos trabajar, en el área de las matemáticas, cada una de las ocho inteligencias que nos propone Gardner.

  • Inteligencia lingüística-verbal: es importante tener en cuenta que las matemáticas no son sólo números y que muchos de los procesos necesarios para la resolución de problemas y conocimiento de los aspectos necesarios de éste área se pueden trabajar a través de la capacidad lingüística y verbal.
    • Crear un programa de radio a través de podcast, en el que los alumnos elaboren diferentes grabaciones con aspectos teóricos, propuestas de juegos de ingenio o contando las historias creadas en la primera actividad propuesta.
    • Inventar eslóganes originales sobre conceptos matemáticos a modo de reglas nemotécnicas para recordar con mayor facilidad los contenidos.
  • Inteligencia lógico-matemática: la inteligencia lógico-matemática va mucho más allá del uso de números, ya que también engloba la capacidad para comprender relaciones lógicas, elaborar enunciados y propuestas a problemas de ingenio o realizar esquemas y abstracciones.
    • Inventar juegos de estrategia en los que estén presentes los contenidos matemáticos adquiridos hasta el momento.
    • Elaborar líneas de tiempo con hechos históricos matemáticos del trabajo realizado en el aula a lo largo del curso a modo de diario de aprendizaje visual.
  • Inteligencia musical: hoy en día la música es uno de los mayores hobbies y entretenimientos de los jóvenes y podemos sacarle muchísimo provecho en nuestras aulas introduciéndola como un elemento más.
    • Crear presentaciones orales que incluyen acompañamiento musical, creado por los alumnos.
    • Escribir letras de canciones sobre los contenidos estudiados.
  • Inteligencia espacial: si trabajamos la capacidad espacial desde principio de curso y de manera constante, temas tan complejos como los de poliedros o movimientos en el plano, en los que los alumnos necesitan tener una visión espacial avanzada, no supondrá mayor complicación.
    • Elaboración de mapas mentales, individuales o grupales, de cada uno de los bloques de contenidos estudiados.
    • Hacer salidas fuera del aula para aprender el uso de la brújula a través de geolocalización, uso de realidad aumentada,…
  • Inteligencia corporal-cinética: muchas veces nos encontramos dentro del aula con niños que se mueven constantemente, hablan y no están quietos mientras trabajan. Quizás esta forma de actuar se debe porque lo necesitan para poder estudiar y aprender. Es aconsejable que el docente propicie este tipo de experiencias dentro del aula para sacar el mayor provecho a las capacidades de estos niños y desarrollar en mayor medida este tipo de inteligencia.
  • Inteligencia interpersonal: gracias a la inteligencia interpersonal somos capaces de relacionarnos con las personas que nos rodean (búsqueda de pareja, de amigos, de trabajo). Nos permite entender a los demás y con ella desarrollamos la empatía y la capacidad de manejar situaciones en las que haya relaciones sociales.
  • Inteligencia intrapersonal: es la primera que se centra en el conocimiento personal y la autoestima del alumno. Muchas veces estamos tan centrados en lo académico que nos olvidamos de esta parte personal y que en gran medida puede determinar el éxito o fracaso de los alumnos. El control de las emociones en los estudiantes es muy importante, no solo durante pruebas escritas, sino en el día a día.
    • Escribir un diario de aprendizaje, en el que los últimos cinco minutos de clase apunte todo lo que ha aprendido y cómo lo ha utilizado. Es importante que el profesor haga un seguimiento y de feedback al alumno.
    • Recibir la opinión de los compañeros acerca de la resolución de problemas o la presentación oral de trabajos relacionados con diferentes temas.
  • Inteligencia naturalista: el desarrollo de esta inteligencia no es diferente de la enseñanza de las matemáticas, de hecho podemos introducir actividades y adaptar nuestras clases para que nuestros alumnos trabajen al máximo esta capacidad de investigación.
    • Explorar el entorno cercano en busca de objetos y símbolos matemáticos. Con todo lo encontrados crear una colección con características de cada uno de los descubrimientos.
    • Crear investigaciones “a lo Sherlock Holmes” en la que los alumnos a través de pistas deben resolver un hecho misterioso investigando por todo el centro escolar.

No debemos olvidarnos que tenemos dentro del aula una gran variedad de alumnos, que no todos son iguales, y que cada uno de ellos aprende y se desarrolla de maneras muy diferentes. Es por ello necesario no centrarnos en el desarrollo de todas estas capacidades por igual en los alumnos, sino en descubrir cuáles son las que tienen más desarrolladas y potenciarlas, sin dejar de lado el resto.

Fuente artículo: http://blog.tiching.com/inteligencias-multiples-y-matematicas/

Comparte este contenido:
Leer más »

Más allá de las tablas de multiplicar

Dácil González Martel

28 de junio de 2017 / Fuente: http://blog.tiching.com

Por: Dácil González Martel

Desde que empezamos la etapa de Educación Primaria nos enseñan las distintas operaciones básicas, la suma, la resta, la multiplicación, la división… Es tan importante el cálculo en nuestro día a día que nos vemos obligados a practicarlo a diario, ya no sólo en la escuela sino en casa o en otras situaciones extraescolares de nuestro día a día.

Cuando enseñamos las tablas de multiplicar hay niños que las memorizan al momento, otros niños consigue dominarlas sumando mentalmente y otros a los que les cuesta tanto que se pasan toda su etapa en Primaria repasándolas.

Según pasan los cursos, la operación de la multiplicación se va complicando, pasamos de multiplicar números simples a números más complejos (naturales, decimales, enteros, fraccionarios,…) y es aquí donde nuestros alumnos en ocasiones se bloquean y no avanzan. Es por ello que queremos proponer otros métodos, de otras culturas, que pueden facilitar mucho el cálculo de nuestros alumnos; así como formas de multiplicar curiosas:

  • Multiplicación maya: los mayas eran grandes matemáticos para los pocos recursos con los que contaban. Su forma de multiplicar era bastante sencilla, rápida y útil. Nos sirve para multiplicar prácticamente cualquier número. Lo hacían a través de línea cruzadas y no es necesario conocer las tablas de multiplicar tal y como las conocemos. Puesdes practicar este método con este sencillo vídeo explicativo.
  • Multiplicación musulmana: a la cultura musulmana les debemos mucho, especialmente los números tal y como los escribimos hoy en día. Para multiplicar utilizaban una cuadrícula y colocaban los números en un orden determinado. Nos puede servir para multiplicar grandes números.  En este vídeo se explica la forma de multiplicar musulmana, utilizando una cuadrícula.TablasMultiPost3

    TablasMultiPost2

    Estas son sólo algunas de las muchas formas de multiplicar que nos podemos encontrar. Nuestra principal misión como docentes es intentar facilitar las cosas a nuestros alumnos y estas formas puede resultar fáciles y divertidas, especialmente para aquellos niños a los que por unas razones u otras les cueste aprenderse las tablas de multiplicar.

  • Multiplicación con círculos: lo curioso de esta forma de realizar la operación es que tan solo debemos dibujar círculos concéntricos y líneas. Al principio puede resultar complicada, pero cuando se le coge el truco facilita mucho las cosas. Para realizarla no hace falta conocer las tablas de multiplicar y es mejor no realizar este método con multiplicaciones de números grandes. Por último este vídeo con la explicación del método para multiplicar dibujando círculos.

TablasMultiPost2

Estas son sólo algunas de las muchas formas de multiplicar que nos podemos encontrar. Nuestra principal misión como docentes es intentar facilitar las cosas a nuestros alumnos y estas formas puede resultar fáciles y divertidas, especialmente para aquellos niños a los que por unas razones u otras les cueste aprenderse las tablas de multiplicar.

Fuente artículo: http://blog.tiching.com/mas-alla-de-las-tablas-de-multiplicar/

Comparte este contenido:
Leer más »

Música y matemáticas: dos geniales compañeros

Dácil González Martel

29 de marzo de 2017 / Fuente: http://blog.tiching.com

Por: Dácil González Martel

La música y las matemáticas tienen algo en común, las dos necesitan de la creatividad para desarrollarse. Además de esto, su relación es muy estrecha, las dos son lenguajes universales, son lenguajes abstractos que requieren de su aprendizaje para poder descifrarlos y ambas buscan la belleza. Ya lo decía Puig Adam: “Tal vez sea la música la matemática del sentido y la matemática la música de la razón”.

El objetivo principal de nuestra labor como maestros es potenciar la situaciones de aprendizaje dentro del aula. En el área de matemáticas no sólo debemos transmitir conocimientos, sino que debemos dejar que el alumno descubra a través de retos, desafíos y problemas cada uno de los conceptos que trabajamos. De esta forma no solo estaremos transmitiendo conocimiento, sino que el alumno desarrollará el pensamiento crítico, el razonamiento y la creatividad haciendo significativo el aprendizaje.

Dentro del tema que nos ocupa, matemáticas y música, podemos encontrar muchas actividades que engloban las dos disciplinas y que ayudan no sólo a perder el miedo a algunos conceptos matemáticos o musicales, sino a desarrollar la creatividad a través de diferentes retos:

  • Operar con figuras musicales: Las figuras con las que se escriben las notas musicales tienen unos valores numéricos que nos proporcionan una excusa perfecta para trabajar series numéricas u operaciones sencillas de cálculo.

Captura de pantalla 2017-01-10 a las 12.48.08

  • Perder el miedo a las fracciones: Hay conceptos musicales como el “puntillo” (es un signo que se coloca a la derecha de la figura y que aumenta la mitad del valor de la misma) que nos ayuda a trabajar la suma de dos fracciones con denominador diferente, pudiendo pedir al alumnos que expresen notas con puntillo como suma de dos fracciones.

Captura de pantalla 2017-01-10 a las 12.50.03

  • Matemáticas y compás musical: Un compás musical es la entidad métrica musical que se coloca entre líneas divisorias y se estructura al comienzo de una obra mediante una fracción cuyo denominador marca las partes en las que se divide la figura redonda y el numerador indica el número de partes que entran en el compás. Podemos proponer a los alumnos que escriban tres compases de manera que los valores de sus notas se corresponda con la suma de una serie de fracciones. También se puede hacer al contrario, darle al alumno un pentagrama con tres compases y pedirle que exprese las notas que aparecen como suma de fracciones.

Captura de pantalla 2017-01-10 a las 12.52.41

  • Jugamos con la música y la matemática: Podemos crear un dominó de sumas y figuras musicales tomando el valor de la corchea como el 1, dos corcheas como 2… También se puede incluir el concepto de suma de fracciones poniendo la equivalencia del valor de las figuras musicales en forma de suma de fracciones.

Captura de pantalla 2017-01-10 a las 12.53.53

El aula de matemáticas debe ser un lugar vivo, con multitud de experiencias vivenciales para el alumno que le hagan desarrollar un pensamiento matemático rico y real. Para conseguir esto, el profesor pasa a un segundo plano y el alumno se convierte en el auténtico protagonista. Como dice José Antonio Fernández Bravo, “se debe partir del cerebro del que aprende y no del cerebro del que enseña”.

Fuente artículo: http://blog.tiching.com/musica-matematicas-dos-geniales-companeros/

Comparte este contenido:
Leer más »

Música y matemáticas: dos geniales compañeros

Dácil González Martel

Por: Dácil González Martel

La música y las matemáticas tienen algo en común, las dos necesitan de la creatividad para desarrollarse. Además de esto, su relación es muy estrecha, las dos son lenguajes universales, son lenguajes abstractos que requieren de su aprendizaje para poder descifrarlos y ambas buscan la belleza. Ya lo decía Puig Adam: “Tal vez sea la música la matemática del sentido y la matemática la música de la razón”.

El objetivo principal de nuestra labor como maestros es potenciar la situaciones de aprendizaje dentro del aula. En el área de matemáticas no sólo debemos transmitir conocimientos, sino que debemos dejar que el alumno descubra a través de retos, desafíos y problemas cada uno de los conceptos que trabajamos. De esta forma no solo estaremos transmitiendo conocimiento, sino que el alumno desarrollará el pensamiento crítico, el razonamiento y la creatividad haciendo significativo el aprendizaje.

Dentro del tema que nos ocupa, matemáticas y música, podemos encontrar muchas actividades que engloban las dos disciplinas y que ayudan no sólo a perder el miedo a algunos conceptos matemáticos o musicales, sino a desarrollar la creatividad a través de diferentes retos:

  • Operar con figuras musicales: Las figuras con las que se escriben las notas musicales tienen unos valores numéricos que nos proporcionan una excusa perfecta para trabajar series numéricas u operaciones sencillas de cálculo.

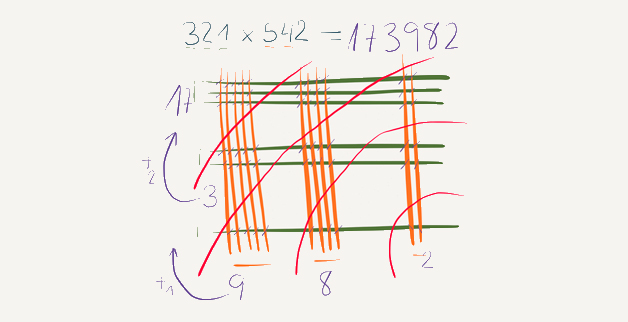
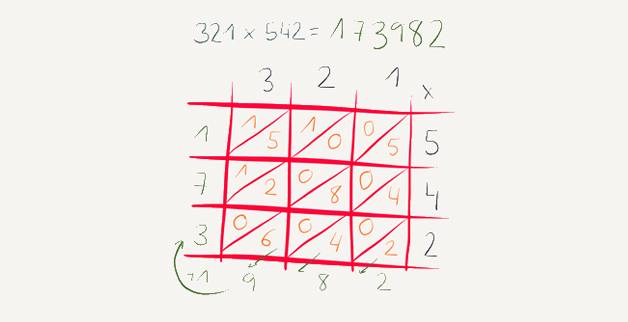
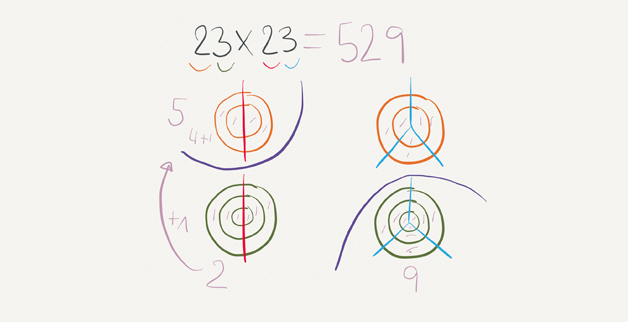
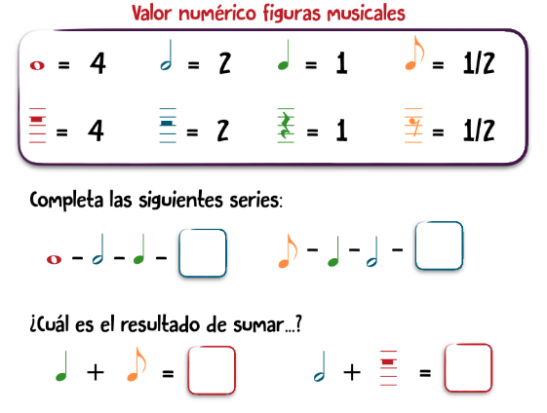
Captura de pantalla 2017-01-10 a las 12.48.08

  • Perder el miedo a las fracciones: Hay conceptos musicales como el “puntillo” (es un signo que se coloca a la derecha de la figura y que aumenta la mitad del valor de la misma) que nos ayuda a trabajar la suma de dos fracciones con denominador diferente, pudiendo pedir al alumnos que expresen notas con puntillo como suma de dos fracciones.

Captura de pantalla 2017-01-10 a las 12.50.03

  • Matemáticas y compás musical: Un compás musical es la entidad métrica musical que se coloca entre líneas divisorias y se estructura al comienzo de una obra mediante una fracción cuyo denominador marca las partes en las que se divide la figura redonda y el numerador indica el número de partes que entran en el compás. Podemos proponer a los alumnos que escriban tres compases de manera que los valores de sus notas se corresponda con la suma de una serie de fracciones. También se puede hacer al contrario, darle al alumno un pentagrama con tres compases y pedirle que exprese las notas que aparecen como suma de fracciones.

Captura de pantalla 2017-01-10 a las 12.52.41

  • Jugamos con la música y la matemática: Podemos crear un dominó de sumas y figuras musicales tomando el valor de la corchea como el 1, dos corcheas como 2… También se puede incluir el concepto de suma de fracciones poniendo la equivalencia del valor de las figuras musicales en forma de suma de fracciones.

Captura de pantalla 2017-01-10 a las 12.53.53

El aula de matemáticas debe ser un lugar vivo, con multitud de experiencias vivenciales para el alumno que le hagan desarrollar un pensamiento matemático rico y real. Para conseguir esto, el profesor pasa a un segundo plano y el alumno se convierte en el auténtico protagonista. Como dice José Antonio Fernández Bravo, “se debe partir del cerebro del que aprende y no del cerebro del que enseña”.

Fuente: http://blog.tiching.com/musica-matematicas-dos-geniales-companeros/

Comparte este contenido:
Leer más »

Visual thinking y matemáticas

Dácil González Martel

07 de diciembre de 2016 / Fuente: http://blog.tiching.com/

Por: Dácil González Martel

“Si no puedes dibujarlo es que no lo entiendes” (Albert Einstein)

Muchas veces, como profesores de matemáticas en Primaria, cuando explicamos conceptos nuevos a nuestros alumnos tales como fracciones, operaciones combinadas, superficies o volúmenes vemos en ellos caras de “esto es un lío”, “no lo entiendo”, “esto es muy abstracto”…

Cuando explicamos conceptos nuevos que nosotros consideramos de “fácil” comprensión, debemos ponernos en el lugar de los niños de 6 a 12 años, adaptando nuestras explicaciones y nuestras actividades a su nivel y su lenguaje.

Aún recuerdo la primera vez que expliqué el concepto de fracción a alumnos de 4º de Educación Primaria. Comencé explicando que una fracción eran las partes iguales que cogemos o dejamos de la unidad. Me quedé mirando las caras de los 26 alumnos, me miraban con extrañeza y, sin decirlo, me estaban pidiendo que volviera a explicarlo. Cogí unas cuantas tizas de colores y realicé un dibujo como el siguiente, ante el cual los alumnos fueron sonriendo y diciendo: “¡Ahora lo entiendo!”

El visual thinking es una herramienta que nos ayuda a expresar ideas a través de dibujos simples con el objetivo de entenderlas mejor, buscar soluciones a problemas, generar nuevas ideas, etc. El 80% de nuestro cerebro asimila y procesa imágenes, por lo que le supone menor esfuerzo que leer un texto. Es por ello que debemos aprovechar dicha capacidad innata a la hora mostrar nuevos conceptos matemáticos a nuestros alumnos.

No hace falta que seamos unos artistas, basta con conocer una serie de formas básicas (punto, cuadrado, triángulo, círculo, línea) y a partir de ellas hacer dibujos sencillos. En el visual thinking no es tan importante la perfección del dibujo, sino la expresión de ideas a través de ellos.

Como profesores podemos utilizar dicha herramienta para explicar conceptos más abstractos, para ayudar al estudio de nuestros alumnos a través de resúmenes o de mapas mentales, para la comprensión de problemas matemáticos…Visual thinking | TichingDebemos animar a nuestros alumnos a realizar visual thinking en sus cuadernos para explicar conceptos, para resolver problemas o ejercicios, a realizar mapas mentales para organizar sus ideas… Los niños de 6 a 12 años aún no tienen prejuicios, dibujan sin parar y sin pensar en el resultado final, aún no ha aparecido en ellos la frase de “yo no sé dibujar”. Es por ello que debemos aprovechar dicha capacidad para enseñarles a aprender a pensar a través de imágenes.

Visual thinking | Tiching

Fuente artículo: http://blog.tiching.com/visual-thinking-y-matematicas/

Comparte este contenido:
Leer más »

Matemáticas cooperativas en Primaria

Dácil González Martel

16 de noviembre de 2016 / Fuente: http://blog.tiching.com/

Por: Dácil González Martel

El aprendizaje cooperativo es una estrategia metodología que se usa, hoy en día, en prácticamente todas las aulas. En ella el grupo tiene que trabajar conjuntamente para conseguir un objetivo que solo se logrará si cada miembro del equipo consigue su propio objetivo. Muchos estudios han demostrado los beneficios del aprendizaje cooperativo dentro del aula, tales como el desarrollo de habilidades interpersonales y trabajo en equipo, fomento de la responsabilidad personal y autoestima, aumento de la motivación en el aprendizaje de nuevos conceptos…

En el aula de matemáticas en educación primaria debemos apostar por un aprendizaje vivencial, manipulativo y explorativo, en el que nuestro papel como docentes se convierte en guía de dicho descubrimiento. El aprendizaje cooperativo jugará un papel primordial y ayudará a los alumnos a sentirse protagonistas de su aprendizaje y con ello su motivación por seguir avanzando crecerá de forma significativa. En nuestro papel de guías deberemos trabajar para que su cumplan los principios básicos que rigen el aprendizaje cooperativo: igual participación, interdependencia positiva, responsabilidad individual y grupal e interacción simultánea.

Existen numerosas técnicas o dinámicas de aprendizaje cooperativo. Os proponemos algunas que podréis utilizar en el aula de matemáticas de primaria para trabajar diferentes contenidos:

  • Lápices al centro: el profesor propone un ejercicio o problema a los alumnos. Cada grupo cooperativo nombra a un moderador. Los alumnos colocan los bolígrafos en el centro de la mesa para indicar que en ese momento se puede hablar y escuchar, pero no escribir. Los moderadores leen en voz alta el problema, se aseguran que todo el grupo expresa su opinión y comprueba que todos comprenden la respuesta acordada. Pasado el tiempo establecido, cada alumno come su lápiz y responde a la pregunta por escrito. En este momento solo se puede escribir, no se puede hablar.
  • Quiz quiz trade: cada alumno dispone de una tarjeta en la que aparece una pregunta del tema por una cara y la respuesta por el otro. El grupo se mueve por la clase (se puede poner música para que se muevan por todo el aula) y cuando el profesor indica se emparejan con otro compañero. Un compañero pregunta al otro, que intenta dar la respuesta correcta. Si no acierta, se le puede dar hasta dos pistas, y si finalmente tampoco consigue acertar, el que ha leído la pregunta le da la solución para que el compañero la aprenda. Una vez que los dos compañeros han preguntado, se intercambian las tarjetas y buscan a otros compañeros que queden libres.
  • El rompecabezas: se divide la clase en grupos heterogéneos de 4 o 5 alumnos cada uno. El material de estudio se divide en tantas partes como miembros tiene el equipo, de forma que cada uno recibe un fragmento de la información del tema. Cada miembro del equipo prepara su parte a partir de información que facilita el profesor o la que él ha podido buscar. Después, con los integrantes de los otros equipos que han estudiado y preparado el mismo punto forman un grupo de expertos, donde intercambian la información y la completan, construyendo esquema y mapas conceptuales. A continuación, cada uno de ellos retorna a su equipo de origen y se responsabiliza de explicar al grupo la parte que él ha preparado.
  • Folio giratorio: el profesor entrega a los grupos un folio con una frase relacionada con los contenidos que se trabajarán durante la sesión. El folio se coloca en el centro de la mesa del grupo y va girando para que cada alumno escriba las ideas que la frase le sugiere. A continuación, los grupos intercambian el folio con otros equipos y añaden ideas que no estén recogidas. Finalmente, cada grupo recoge su folio con las aportaciones de otros grupos y trata de construir una idea general sobre la frase que pondrán en común con todo el grupo.
  • Parejas cooperativas para la resolución de problemas: exponemos a los alumnos una situación problema, los alumnos por parejas dialogan sobre la misma tratando de responder a preguntas tales como cuál es el problema, qué nos preguntan o qué datos tienen para resolverlo. Después, de forma individual buscan diferentes vías para resolverlo utilizando los materiales que necesiten. Pasado un tiempo, lo ponen en común y eligen uno de los posibles caminos y elaboran un plan con pasos para llegar a la solución final. El profesor, finalmente elige al azar a algunos alumnos para que explique a todo el grupo la solución y el proceso que han seguido para conseguirla.

Fuente artículo: http://blog.tiching.com/matematicas-cooperativas-en-primaria/

Comparte este contenido:
Leer más »