Mª Ángeles García Ferrero, premio José Luis Rubio de Francia.
Se licenció en Física, pero sus ecuaciones para describir la evolución del calor le han llevado a ganar uno de los premios más prestigiosos para los jóvenes matemáticos de nuestro país. Ahora trabaja en el Instituto de Matemática Aplicada de la Universidad de Heidelberg, en Alemania.
Este año la Real Sociedad Matemática Española (RSME) ha concedido a María Ángeles García Ferrero (León, 1991) el Premio José Luis Rubio de Francia, dirigido a investigadores matemáticos menores de 32 años y dotado con una start-up grant de 35.000 euros financiada por la Fundación BBVA.
«Todavía no he pensado qué voy a hacer con esta beca, pero supongo que una parte será para continuar colaborando y trabajando de forma presencial, porque las videollamadas están muy bien pero a veces son limitadas», comenta la galardonada.
El Premio José Luis Rubio de Francia reconoce sus resultados de aproximación global a la ecuación del calor, logrados con la ayuda de ecuaciones en derivadas parciales
García Ferrero se licenció en Física en la Universidad de Valladolid, se doctoró en Matemáticas en la Universidad Complutense de Madrid y luego obtuvo una plaza de investigación postdoctoral en el Instituto Max Planck de Matemáticas en las Ciencias de Leipzig (Alemania), aunque recientemente se ha trasladado al Instituto de Matemática Aplicada de la Universidad de Heidelberg.
¿Te sientes más física o matemática?
Las dos cosas un poco y ninguna del todo. Durante la carrera de Física, era la matemática del grupo. Me sentía más cómoda cuando podía trabajar solo con papel y lápiz. En quinto, hablando con un compañero, me di cuenta de que nuestras motivaciones y formas de estudiar un problema de partículas elementales eran totalmente distintas: yo necesitaba trabajar con ecuaciones. Pero reconozco que no he seguido una formación completa en matemáticas.
¿Qué ha supuesto el premio José Luis Rubio de Francia?
Un honor y un gran estímulo para seguir trabajando e intentar emular a premiados anteriores y a muchos otros colegas a los que admiro. Me hace ilusión también porque reconoce el buen hacer de mi director de tesis y del resto de investigadores con los que he tenido la suerte de trabajar. Pero como cualquier otro reconocimiento, genera un conflicto entre mi inseguridad y el juicio externo.
Eres la segunda mujer en conseguirlo ¿cómo ves la situación actual de la mujer en la ciencia, especialmente en matemáticas?
«La mayoría de mis compañeros son hombres y si miras hacia puestos de mayor trayectoria, el porcentaje de mujeres aún es menor; lo preocupante es que está volviendo a decrecer su número en las etapas iniciales»
La mayoría de mis compañeros son hombres y si miras hacia puestos de mayor trayectoria, el porcentaje de mujeres aún es menor. Pero lo preocupante es que está volviendo a decrecer el número en las etapas iniciales. La inestabilidad asociada a esta profesión, especialmente en España, hace más mella en las mujeres. Además los criterios de evaluación a menudo tampoco contemplan hechos como la maternidad.
¿Las desigualdades de género siguen ahí…?
Los prejuicios supongo que tienen más peso en edades tempranas. Lamentablemente, muchas niñas asumen que las matemáticas o las asignaturas más tecnológicas no se le dan bien, y durante la carrera más chicas creen no encajar en el mundo académico. A mí nunca me dijeron que no podía dedicarme a esto, o si lo hicieron hice oídos sordos. En mi caso nunca he sentido ningún comportamiento negativo por ser mujer, pero sí conozco malas experiencias de compañeras.
En lenguaje sencillo, ¿en qué consiste la aproximación global para la ecuación de calor por la que has sido premiada?
«Si nos situamos en una habitación sin radiadores ni aire acondicionado, podemos encontrar en cada momento puntos donde la temperatura es más alta que en los puntos de alrededor»
Imagina que tienes una distribución de temperatura que evoluciona según la ecuación del calor en una zona del espacio y en cierto intervalo de tiempo. El resultado de aproximación más general lo que nos dice es que es posible encontrar una distribución de temperatura que obedece a esa misma ecuación pero en una zona mayor, o incluso todo el espacio. Además (ya para especialistas), ambas distribuciones se parecen tanto como queramos en la región de partida durante ese intervalo de tiempo.
¿En qué ámbito se puede aplicar?
Si nos situamos en una habitación sin radiadores ni aire acondicionado, podemos encontrar en cada momento puntos donde la temperatura es más alta que en los de alrededor. Si lo representamos en una imagen, no solo son los puntos rojos, sino aquellos otros donde el color es más cálido que alrededor. La temperatura irá variando con el tiempo, e igualmente la localización de estos puntos podrá cambiar. Con los resultados de aproximación probamos que podemos prescribir el movimiento de estos puntos si elegimos adecuadamente la temperatura inicial y la de las paredes.
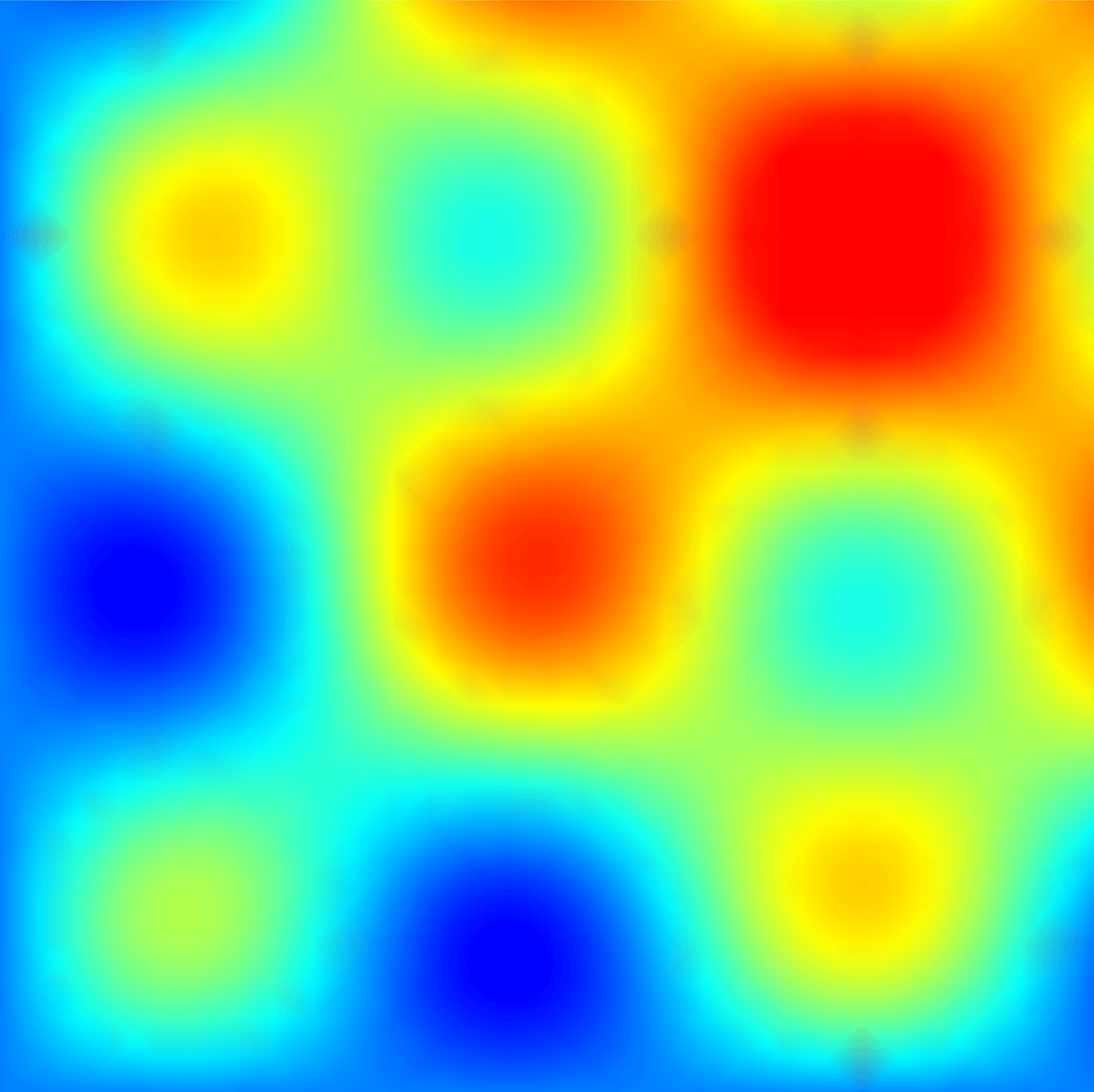
Imagen para ilustrar el concepto de puntos calientes locales. / M. A. García-Ferrero
De forma análoga podemos prescribir también la forma de las superficies isotermas, es decir, puntos con la misma temperatura. Con la ecuación del calor y otras ecuaciones parabólicas se pueden modelar otras magnitudes. Estos resultados serían igualmente válidos cambiando los puntos calientes por máximos locales con esas magnitudes.
Este trabajo lo desarrollaste en el Instituto de Ciencias Matemáticas…
Sí, en el ICMAT, con mi director de tesis, Alberto Enciso, y Daniel Peralta-Salas, que ha sido como otro director aunque no figure en los papeles. Los dos iniciaron la idea de utilizar los resultados de aproximación para estudiar propiedades topológicas o geométricas, como qué aspecto puede tener la curva donde una función tiene el mismo valor. Con ellos también he trabajado en mecánica de fluidos, en concreto, estudiando líquidos o gases ideales encerrados en un recipiente.
«Los modelos ayudan a luchar contra las pandemias, pero eso no significa que den respuestas exactas en todo momento, ya que no es posible contemplar todas las variables»
¿En qué otros campos estás interesada?
También trabajo con polinomios ortogonales, que aparecen por ejemplo en mecánica cuántica. Además, se utilizan para aproximar funciones más complejas y hacer operativo el análisis numérico. En particular, me centro en los llamados polinomios excepcionales junto con David Gómez-Ullate y Robert Milson. Me interesa sobre todo su clasificación y la construcción de familias nuevas.
¿Y ahora qué investigas en Alemania?
En el Instituto Max Planck y actualmente en la Universidad de Heidelberg he continuado con resultados de aproximación pero para ecuaciones no locales, en las que el valor en un punto no depende únicamente del comportamiento de la función en un entorno del mismo. Estas ecuaciones aparecen en numerosas aplicaciones de física, biología y economía. También he empezado a trabajar en problemas inversos, aquellos en los que se pretende conocer parámetros de la ecuación a partir de datos observados, algo habitual en física y, por ejemplo, crucial en el diagnóstico médico.
¿Cómo has vivido allí estos meses de pandemia?
En Alemania ha sido más leve porque en todo momento se ha podido salir a caminar o a hacer deporte. A mí me tocó mudarme a Heidelberg a comienzos de abril, así que me fui de Leipzig sin poderme despedir de mis amigos y compañeros, para llegar a un lugar donde apenas he podido hablar con gente. Al principio, la preocupación y la incertidumbre no me dejaban trabajar bien. Después, el propio trabajo ha conseguido abstraerme de todo lo demás.
¿Crees que los modelos matemáticos ayudan a luchar contra pandemias como esta?
Los modelos ayudan sin duda, pero eso no significa que nos tengan que dar respuestas exactas en todo momento. No es posible contemplar todas las variables en el modelo, y estas están sujetas a muchos cambios.
¿Cuándo empezó tu pasión por las matemáticas?
Las matemáticas me han gustado desde el colegio. Aparte de cierta inclinación natural, que no tenía por ejemplo para memorizar, tuve muy buenos profesores de matemáticas, que además me dejaban pelearme con problemas fuera del temario.
«Una aproximación desde el mundo tecnológico en el que vivimos haría más atractiva la asignatura de las matemáticas»
¿Hasta qué punto las matemáticas son importantes en la formación de una persona?
El papel más importante de las matemáticas en la enseñanza ha de ser el de desarrollar un sentido crítico y lógico. Además, sería deseable que igual que la asignatura de música puede crear cierta sensibilidad sin necesidad de ser experto, se creara cierta sensibilidad hacia la importancia de las matemáticas en el desarrollo de la sociedad.
¿Algún consejo para acabar con su mala fama entre muchos estudiantes?
La metodología de memorizar fórmulas o recetas para resolver veinte ejercicios iguales desanima a los estudiantes y no muestra cómo funcionan las matemáticas en realidad. Por eso cuando ayudo a algún chaval con los deberes siempre prefiero los problemas, donde la resolución es solo una parte y primero hay que hacer un ejercicio de comprensión, y luego de traducción al lenguaje matemático. Una aproximación desde el mundo tecnológico en el que vivimos también haría más atractiva esta asignatura.
Además diría a los adultos que dejen de cargarle esta mala fama. Si los niños escuchan a sus padres preguntarse de qué les ha servido en la vida aprender a hacer una raíz cuadrada, probablemente la desgana aumente. Es normal olvidar la mayoría de fechas que hemos estudiado en historia, y no por ello aprenderlas en su momento y los posos que quedan la hacen despreciable.

María Ángeles García Ferrero trabaja actualmente en Alemania con ecuaciones que se podrían aplicar en física, biología y economía. / Foto cortesía de la entrevistada
Fuente e Imagen: https://www.agenciasinc.es/Entrevistas/Las-matematicas-te-ayudan-a-desarrollar-un-sentido-critico-y-logico

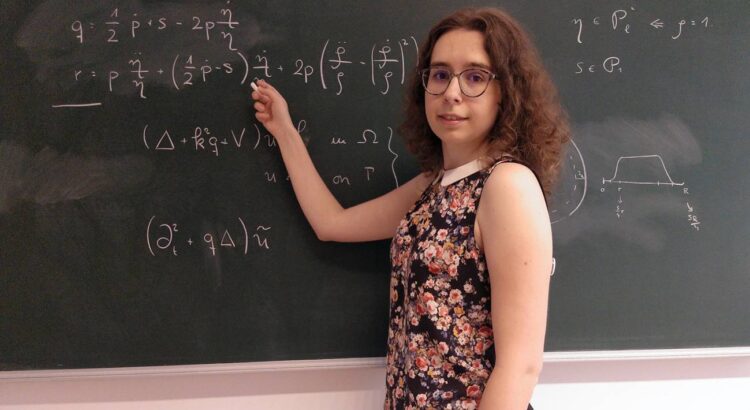












 Users Today : 7
Users Today : 7 Total Users : 35460216
Total Users : 35460216 Views Today : 10
Views Today : 10 Total views : 3418905
Total views : 3418905