Por: Semana
Para algunos las matemáticas es una ciencia placentera mientras que para otros resulta una pesadilla. Y si de multiplicación se trata, ¿sabía usted que existen otros métodos alternativos al tradicional? Acá le contamos tres de ellos. Eso sí, deberá tener buen pulso para líneas, círculos y cuadros. ¿Se anima a dibujar?.
«Las matemáticas son complicadas».
Seguramente ha escuchado esta frase muchas veces o incluso, tal vez, salió de su propia boca.
Lo cierto es que para algunos las matemáticas es una ciencia placentera mientras que para otros resulta una pesadilla (claro siempre está la calculadora como salvación).
Pero centrémonos en un solo aspecto de las matemáticas: la multiplicación.
Es probable que el método para multiplicar que usted haya aprendido en la escuela fuese el tradicional. Es decir, primero aprende las tablas de multiplicar de memoria para luego resolver los cálculos número tras número.
Y si las cifras a multiplicar tienen varios dígitos, necesitarás de un largo trozo de papel para resolverla.
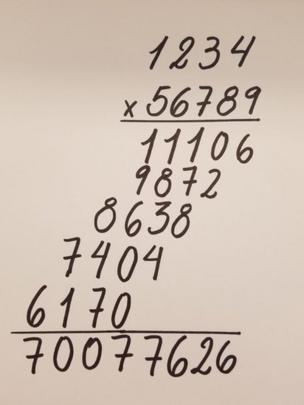
Pero si esta larga lista de líneas numéricas, una debajo de la otra, le resulta difícil de interpretar, existen otras alternativas para resolver un cálculo matemático.
Y aquí es donde aparecen tus habilidades artísticas.
A dibujar
Entre los numerosos y variados métodos de multiplicación que existen al menos tres de ellos requieren líneas, puntos y cuadrados.
1. El método maya, también conocido como japonés
Hay varias teorías sobre el origen de este método.
Unas sugieren que fue inventado por la civilización maya que habitaron América Central hasta la llegada de los conquistadores en el siglo XV. Y es conocido como método japonés porque los profesores de ese país utilizan esta multiplicación visual con líneas para enseñar a los alumnos de primaria.
Consiste en dibujar rectas paralelas y perpendiculares para representar los dígitos de los números a multiplicar.
Tomemos por ejemplo 23 x 41.
Dibujamos dos líneas paralelas para representar el 2 y otras tres líneas paralelas para el 3.
Luego perpendicularmente dibujamos cuatro líneas paralelas para el 4 y una línea para el 1.
A continuación, una vez que tenemos nuestra imagen, se suman los puntos que se forman en las intersecciones.
Y así obtenemos como resultado 943, el mismo que la forma tradicional de multiplicar.
¿Le resultó difícil?
2. Método de multiplicación hindú o de celdillas o de gelosia
Tampoco está claro el origen del método de multiplicación hindú, pero marcó su paso por Asia.
«El algoritmo de las gelosias (celosías en español) fue transmitido de India a China y a Arabia, de aquí hacia Italia durante los siglos XIV y XV, donde recibió el nombre de gelosia, debido al parecido que tenía con las persianas venecianas», según detalla Mario Roberto Canales Villanueva, en su Estudio Exploratorio sobre el uso de Modelos Alternativos para la Enseñanza y Aprendizaje de la Multiplicación en Honduras.
En este método de multiplicación tenemos que construir una tabla.
Vamos a usar el mismo ejemplo de antes: 23 x 41.
Entonces, dibujamos una tabla con cuatro casilleros: uno por cada dígito que tenemos en nuestro cálculo.
Y partimos cada cuadro con una línea oblicua.
Entonces empezamos multiplicando los primeros dígitos de ambos números: el 2 con el 4, colocando un 0 en el primer triángulo y un 8 en el segundo.
Luego multiplicamos el 2 con el 1 y colocamos el 0 en el primer triángulo y el 2 en el segundo.
Y hacemos lo mismo con los dos dígitos del segundo número de nuestro cálculo.
Una vez que tenemos todos los casilleros completos, hacemos una suma en diagonal.
Es decir, el primer número será 0, el segundo será un 9, el tercero será un 4 y el último será un 3.
Por lo tanto, el resultado es 943.
¿Fue más fácil?
Vamos con el último método de multiplicación con dibujos.
3. Método de formación operacional (array, en inglés)
En este caso, como en el anterior, necesitamos una grilla o cuadrícula.
Seguimos con el ejemplo 23 x 41.
Aquí descomponemos el número. Es decir en un cuadro colocamos 20 y en el otro 3.
Mientras que en los cuadros verticales colocamos 40 en el primero y 1 en el segundo.
Entonces multiplicamos los números de cada casillero con el contrario.
Sin embargo, ignoramos si hay 0.
Por lo tanto, en vez de multiplicar 20 x 40, suprimimos los 0 y solo calculamos 2 x 4 obteniendo 8.
Lo mismo con 3 x 40. Eliminamos el 0 y multiplicamos 3 x 4 que nos da como resultado 12.
Hacemos lo mismo con los casilleros de abajo.
Y ahora sumamos los 0 que habíamos dejado de lado.
Entonces al primer cálculo que era 20 x 40 y obtuvimos 8, le sumamos dos ceros y nos da 800.
Al 3 x 40 que nos dio 12, le agregamos un 0 y nos queda 120.
Y así sucesivamente con el resto de los casilleros en los cuales suprimimos anteriormente los 0.
Y finalmente sumamos los cuatro números que nos quedaron como resultado en cada uno de los casilleros.
¿Mejoró su comprensión?
Diversidad
Lo concreto es que con todos estos métodos se llega al mismo resultado y en todos ellos se realiza multiplicaciones, por más complejo que te resulte esa operación matemática.
Pero ¿por qué estos métodos no se suelen enseñar en América Latina?
«La historia dice que con el correr de los años se fueron dejando de lado estos métodos porque se le dio mucho más importancia al cálculo mental en América Latina», le dice a BBC Mundo Andrea Vázquez, profesora de matemáticas en Argentina, que entrena a estudiantes para participar en concursos nacionales de esa ciencia.
Pero, David Wees, profesor de matemáticas canadiense y asesor en New Visions for Public Schools, una organización que brinda apoyo educativo a las escuelas públicas de Nueva York, Estados Unidos, tiene otra versión de los hechos.
«Recientemente leí que la razón por la cual el método de multiplicación tradicional es de la forma en que es para ahorrar tinta y el papel. No estaba destinado a ser más fácil de usar, sino a preservar recursos ya que cuando se inventó, la tinta y el papel escaseaban», cuenta Wees.
Pese a ello, piense que los métodos alternativos son útiles.
«Creo que no es una buena práctica llevar a los estudiantes directamente a la multiplicación obligándolos a recordar las tablas de multiplicación sin explicarles de dónde vienen, porque si se olvidan de una, ¿cómo pueden calcular cuál es la siguiente?».
«El método de multiplicación japonés (o maya) es bastante necesario porque con él se puede reconocer la estructura general de la multiplicación y eso podría ser un buen comienzo», afirma Wees a BBC Mundo.
Existen otros métodos de multiplicación matemática bastante diferentes al método tradicional como el ruso o el egipcio, entre otros, aunque no se requiere la habilidad extra de dibujar.
Y según los especialistas consultados, para muchos pueden ser útiles para mejorar la compresión del proceso de multiplicación.
«Obviamente todo ayuda. La matemática en el mundo de hoy es abierta dentro y fuera de las aulas», asegura Vázquez.
Fuente: http://www.semana.com/educacion/articulo/3-sencillos-metodos-para-aprender-a-multiplicar-sin-calculadora/548308






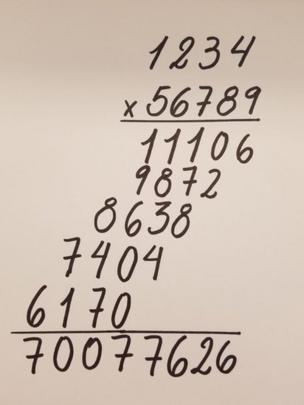







 Users Today : 7
Users Today : 7 Total Users : 35460270
Total Users : 35460270 Views Today : 8
Views Today : 8 Total views : 3418976
Total views : 3418976